References

The relay satellite in Geostationary Neptune Orbit (GNO) is the heart of the communications link between the probes and the Earth. The satellite will act as a data gatherer and will transmit this data to the Earth whenever the satellite is in view of the Earth. The satellite has been decided to be placed in equatorial orbit; the distance required for GNO is determined with the mass and period of Neptune:

$FormBox[RowBox[{T, =, RowBox[{(2 π R^(3/2))/μ^(1/2) R, =, RowBox[{((Tμ^(1/2))/(2π))^2/3, =, RowBox[{8.35039, ×, 10^7, m}]}]}]}], TraditionalForm]$

The radius of GNO was calculated to be 83,503.9 km, approximately three times the equatorial radius. As a result of this large distance, the satellite will have to travel at 9.04706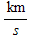in order to maintain its orbit and not be sucked in by Neptune's gravity. Figure 1 shows a diagram of Neptune with a geostationary orbit.

[Graphics:/mathematica/HTMLFiles/index_6.gif]

Figure 1: Geostationary Neptune Orbit

While the distance of free space between the satellite and the 0° probe can be calculated simply by subtracting the GNO radius and the equatorial radius, calculating the distance to the off-angle probes requires the use of the law of cosines

$R_probe = (R_equatorial^2 + R_GNO^2 - 2R_equatorialR_GNOCos(45°))^(1/2)  FormBox[RowBo ... bsp; , RowBox[{= 68, ,, RowBox[{676.7, , km}]}]}], TraditionalForm]$

The angle from the relay satellite to the off-angle probe can be determined by

$FormBox[RowBox[{Angle, =, RowBox[{cos^(-1)((R_probe^2 - R_equatorial^2 + R_GNO^2)/(2 R_probe R_GNO)), =, RowBox[{14.8606, °}]}]}], TraditionalForm]$

This angle is important so that we can choose a dish antenna whose Half-Power Beamwidth (HPBW) will be close to approximately 30°.

The bit error rate (BER) determines the probability that a bit has incorrectly been received at the receiver that defines the quality of a digital communications system, much like the carrier to noise ratio in an analog system [1]. The statistical probability that a bit is incorrect often uses the Q-function, which is a "normalized form of the cumulative normal distribution function giving the probability that a variate assumes a value in the range " [2]. The Q-function is defined by

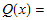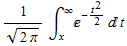
For an uncoded bi-polar phase shift keying (BPSK) signal, the BER is determined by

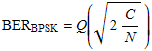
BER_BPSK = Q((2C/N)^(1/2))

where 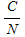is the carrier to noise ratio at the receiver in linear form. Using a turbo code method of forward error correction essentially allows for an error-free communications link if the received 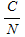is greater than about 1 or 2 dB (see Penetrating Probes » Design).

Next Section »

References:
1. Pratt, Bostian, Alnutt. Satellite Communications, Second Edition. Copyright 2003.
2. Wolfram MathWorld (http://mathworld.wolfram.com/NormalDistributionFunction.html)

top of page

William W
e-mail