|
Calculations
The associated gain of a DSN antenna is determined by, with a diameter of 34m and an efficiency η = 0.94,
![FormBox[RowBox[{G, =, RowBox[{(4π(ηπR)^2)/λ^2, =, RowBox[{RowBox[{RowBox[{ ... }]}], =, RowBox[{RowBox[{8.47001, ×, 10^6}], =, RowBox[{69.2788, , dB}]}]}]}]}], TraditionalForm]](/mathematica/Supplement2/HTMLFiles/index_1.gif)
Similarly, the gain of the relay satellite antenna, with a diameter of 4m and an efficiency of η = 0.85, is determined to be 50.2534 dB.
The power of the radio transmission will be about 100 W, the same as the probes. Performing the link budget analysis, the signal power received at the Earth DSN dish is
![P_receiver = P_transmitter + G_transmitter + 20 log_10(λ/(4 π r)) + G_receiver ɯ ... Box[{-, 164.672}], , dB}], , =, , RowBox[{3.55531, ×, , 10^(-17), W}]}]}]}], TraditionalForm]](/mathematica/Supplement2/HTMLFiles/index_2.gif)
The bandwidth of the signal was increased to approximately 50 kHz due to the additional redundancies of the turbo coding correction. With a 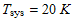 , the DSN antennas will introduce a noise of , the DSN antennas will introduce a noise of
![N_receiver = (k) (T_sys) (B) FormBox[RowBox[{ &nbs ... {RowBox[{2.07099, ×, 10^(-17), W}], =, RowBox[{RowBox[{-, 166.838}], dB}]}]}]}], TraditionalForm]](/mathematica/Supplement2/HTMLFiles/index_4.gif)
The Carrier to Noise ratio can then be determined by
![FormBox[RowBox[{(C/N) _dB, =, RowBox[{RowBox[{10, , RowBox[{log_10, (, RowBox[{RowBox[{(, Row ... [{(, RowBox[{2.07099, ×, 10^(-17)}], )}]}], )}]}], =, RowBox[{2.347, , dB}]}]}], TraditionalForm]](/mathematica/Supplement2/HTMLFiles/index_5.gif)
In any digital link it is important to determine the BER. The total 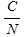 ratio received at NASA's Deep Space Network was 2.347 dB. If this signal contained no error correction, the BER would be ratio received at NASA's Deep Space Network was 2.347 dB. If this signal contained no error correction, the BER would be
![FormBox[RowBox[{BER_BPSK, =, RowBox[{RowBox[{Q, (, RowBox[{RowBox[{(, RowBox[{2, RowBox[{(, Ro ... 347, /, 10}]}], )}]}], )}], ^, (1/2)}], )}], =, RowBox[{3.1944, ×, 10^(-2)}]}]}], TraditionalForm]](/mathematica/Supplement2/HTMLFiles/index_7.gif)
With such a low carrier to noise ratio, approximately 1 in every 32 bits would be lost. However, error correction was used, which essentially yields in a BER of 0; from Figure 2 in Section Penetrating Probes » Design, the BER for a rate 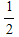 turbo code is extremely low for any turbo code is extremely low for any 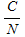 above 1 dB. A rate above 1 dB. A rate 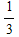 turbo code was used, resulting in more coding gain; therefore, an error-free communications channel can be assumed. turbo code was used, resulting in more coding gain; therefore, an error-free communications channel can be assumed.
Next Section »
References: |


