|
Link with Earth
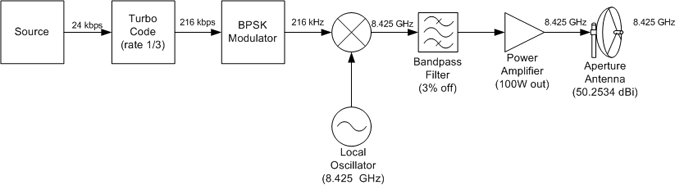
Figure 1: Block Diagram for Relay Satellite Transmitter
Figure 1 shows the block diagram of the communications transmitter for the relay satellite. The source of data will be coming from the solid state hard drives that act as a buffer between the incoming data from the probes and the outgoing data to the Earth.
It is the responsibility of the relay satellite receiver to transmit the data from all three probes safely back to the Earth with no data loss. The maximum distance from Neptune to Earth is 4.6 billion kilometers. At a data rate of 24 kbps, the free space propogational losses will be very large; in fact, the power of the noise might in fact be larger than the carrier power.
Therefore, large amounts of forward error correction must be implemented in order to recover the data completely from such a low received power level. Using error correction increases the bandwidth of the signal, but does not require an increase in the transmitted power. Error correction is responsible for the success of such Deep Space missions such as the Voyager probe; at a distance of over 11 billion kilometers, the Voyager probe is still able to communicate with the Earth by transmitting at a power of 100 W.
The Shannon Channel Capacity theory describes the maximum possible efficiency of error-correcting methods versus levels of noise interference [1]. This capacity is described by
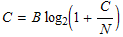
where C is the maximum true data rate of a channel, B is the bit rate, and C/N is the uncoded carrier to noise ratio. By tweaking around with this relationship, knowing that C is constant at 24 kbps, it is possible to obtain a substantial coding gain which will allow the signal to be decoded more easily at the receiver. Performing a quick link budget calculation for the uncoded C/N ratio revels that a bit rate of
Aside from the forward error correction, BPSK modulation is chosen due to its effectiveness in decoding, especially in slower data rates such as the one from the relay satellite to the Earth. Choosing BPSK over QPSK prevents the need to worry about large amounts of fading which could cause a phase shift from one symbol "quadrant" to the other, creating an error.
The carrier frequency used will use the X-Band part of the radio spectrum, which ranges from about 8.2 to 8.7 GHz. Referring to the Frequency Spectrum Chart provided by the DoC [2], there is a special 50 MHz band within the X-Band range that is allocated for use by Deep Space research only. As a result, the relay satellite will be configured to utilize about 75 kHz of this allocated bandwidth by using extra coding in order to overcome the large losses as the signal travels through space. The Shannon limit states that at the same uncoded C/N ratio at a bit rate of 24 kbps, that the maximum data rate achievable would be about 78000 kbps, about 3 times the data rate of the relay satellite. Therefore, to ensure a near-perfect communications channel, a rate 1/3 turbo code will be utilized, providing ample coding gain at the receiver.
Although many other Deep Space projects use this same frequency range, there usually is no interference because the Deep Space Network that is operated by NASA can aim their 34-meter dishes at the relay satellite with pinpoint accuracy and lock onto the transmitted signal.
Unlike the probes falling into the Neptunian atmosphere, Doppler shifting is an important factor in maintaining a communications link with Earth. Both the Earth and Neptune are in orbit around the Sun; the relay satellite is also in orbit around Neptune. This constantly changing distance can add up to several kilometers per second or more. Considering only the speed of the relay satellite around Neptune, the associated Doppler shift is
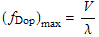 = =![FormBox[RowBox[{RowBox[{RowBox[{(, RowBox[{RowBox[{±, 9.04706}], km/s}], )}], /, RowBox[{(, RowBox[{0.035584, m}], )}]}], =, ± 254247Hz}], TraditionalForm]](/mathematica/HTMLFiles/index_32.gif)
With the motion of the planets, the Doppler shifting may cause a frequency deviation in the upwards of several megahertz. To correct this, NASA has developed a technique called an Ultra-Stable Oscillator (USO) that allows NASA engineers to accurately determine what the transmitted frequency is [3]. The relay satellite will implement a similar plan; advanced navigation packages that are included in the satellite's computers allows the satellite to know where in space it is in relation to the Earth. Using a voltage-controlled oscillator, a feedback loop can use the software's location and the speed to or from the Earth and control the frequency of the oscillator to ensure a constant frequency will be received on the Earth.
Powering the satellite will be a radioisotope thermoelectric generator (RTG). It uses radioactive material (plutonium-238) to produce heat, which is converted to electricity [4]. A single RTG can produce up to 285 W of power, which should provide ample energy to the onboard computer systems as well as provide the 100 W of power for radio communications.
Next Section »
References:
1. Shannon-Hartley Theorem (http://en.wikipedia.org/wiki/Shannon_capacity)
2. Department of Commerce Frequency Allocation (http://www.ntia.doc.gov/osmhome/allochrt.pdf)
3. Cassini Operations and Navigation (http://saturn.jpl.nasa.gov/mission/nav-uso.cfm)
4. Cassini Power System (http://www.planetary.org/html/news/Cassini/hot-top-cassini3.html) |


