|
Calculations
As determined in Penetrating Probes » Calculations , the power received at the receiver antenna is -159.468 dB. Because such a small power is received, noise is an issue and must be taken into consideration. The carrier powers will be determined separately of the noise, and then an overall C/N ratio will be calculated. The despreading gain is not immediately determined.
The dish antenna used provides 15.2638 dBi of gain, therefore the power of the signal after the antenna is
![P_1 = P + G_antenna FormBox[RowBox[{ , RowBox[{=, ... 59.468}], , +, , 15.2638}], , =, , RowBox[{RowBox[{-, 144.204}], dB}]}]}]}], TraditionalForm]](/mathematica/HTMLFiles/index_22.gif)
The LNA offers 27 dB of gain:
![FormBox[RowBox[{P_2, =, RowBox[{P_1 + 27, =, RowBox[{RowBox[{-, 117.207}], dB}]}]}], TraditionalForm]](/mathematica/HTMLFiles/index_23.gif)
Neither the multiplier nor the bandpass filters provide any gain. Therefore, the power going into the BPSK demodulator is
![FormBox[RowBox[{P_3, =, RowBox[{P_2 + 0 + 0, =, RowBox[{RowBox[{RowBox[{-, 117.204}], , dB}], , =, , RowBox[{1.90383, ×, 10^(-12), W}]}]}]}], TraditionalForm]](/mathematica/HTMLFiles/index_24.gif)
The primary sources of noise occur at the receiver, especially with the receiving dish pointing at Neptune, yielding a noise temperature of about 300K. The noise will be determined up to the BPSK demodulator.
![FormBox[RowBox[{N_1, =, RowBox[{RowBox[{(k), (76K + 300K), RowBox[{(, RowBox[{2.046, MHz}], )}]}], =, RowBox[{1.06213, ×, 10^(-14), W}]}]}], TraditionalForm]](/mathematica/HTMLFiles/index_25.gif)
The incoming noise is also amplified by the LNA in addition to adding more noise to the system.
![FormBox[RowBox[{N_2, =, RowBox[{(N_1) (10^27/10) + (k) (61K) (2MHz), =, RowBox[{5.32501, ×, 10^(-12), W}]}]}], TraditionalForm]](/mathematica/HTMLFiles/index_26.gif)
Lastly, the bandpass filters add a total of 36.214K to the system, resulting in a noise power at the BPSK demodulator of
![FormBox[RowBox[{N_3, =, RowBox[{RowBox[{N_2, +, RowBox[{(k), RowBox[{(, RowBox[{36.214, K}], ) ... [{RowBox[{5.32603, ×, 10^(-12), W}], =, RowBox[{RowBox[{-, 112.736}], dB}]}]}]}], TraditionalForm]](/mathematica/HTMLFiles/index_27.gif)
The carrier to noise ratio up to the BPSK demodulator is determined by
![FormBox[RowBox[{(C/N) _dB, =, RowBox[{RowBox[{10, RowBox[{log_10, (, RowBox[{RowBox[{(, RowBox ... 32603, ×, 10^(-12), W}], )}]}], )}]}], =, RowBox[{RowBox[{-, 4.46776}], dB}]}]}], TraditionalForm]](/mathematica/HTMLFiles/index_28.gif)
The despreading gain is proportional to the chip rate to the data rate, but is also affected by the power received. Therefore, the total C/N ratio after despreading is
![(C/N) _despread = (C/N) _dB + 10log_10((M × P_3)/(N_3 + (numProbes - 1) P_3)) FormBox ... p; , RowBox[{=, , RowBox[{6.78386, dB}]}]}], TraditionalForm]](/mathematica/HTMLFiles/index_29.gif)
This C/N ratio is sufficient in order to provide an error-free communications channel. Notice how the signal had a lower power than the noise, but the despreading gain allows the signal to be "pulled out" from under the noise and be processed.
In any digital link it is important to determine the BER. The total 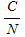 ratio received at the receiver from the probe was 6.78386 dB. If this signal contained no error correction, the BER would be ratio received at the receiver from the probe was 6.78386 dB. If this signal contained no error correction, the BER would be
![FormBox[RowBox[{BER_BPSK, =, RowBox[{RowBox[{Q, (, RowBox[{RowBox[{(, RowBox[{2, RowBox[{(, Ro ... 6, /, 10}]}], )}]}], )}], ^, (1/2)}], )}], =, , RowBox[{1.007, ×, 10^(-3)}]}]}], TraditionalForm]](/mathematica/Supplement1/HTMLFiles/index_10.gif)
This means that approximately 1 in 993 bits would result in an error. For such an important data link, this is unacceptable. Fortunately, a turbo coded error correction scheme was used. From Figure 2 in Section Penetrating Probes » Design, the BER for a rate 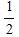 turbo code is extremely low for any turbo code is extremely low for any 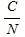 above 1 dB. Therefore, an error-free communications channel can be assumed. above 1 dB. Therefore, an error-free communications channel can be assumed.
Next Section »
References: |


